Multilayer perceptrons in Stata

In this post I introduce an unofficial Stata command, mlp2, for specifying and learning a certain class of neural networks - multilayer perceptrons with 2 hidden layers. Despite their simplicity they turn out to be effective in solving many statistical and machine learning problems, as I hope to show in other posts.

The mlp2 command can be installed by typing the following in Stata:

To see the help file, type

The mlp2 has 3 subcommands: fit - for training a model, predict - for performing prediction on test or validation data using already trained model, and simulate - for simulating new outcome. These commands reflect the typical fit-and-predict approach of most machine learning frameworks.

Model description

The perceptron is a computational model designed to be a simple representation of the biological neuron, [¹]. It takes \(p\) input variables \(x_i\) and produces a single binary output \(y\), according to the function \(y = f(b+\sum_{i=1}^p w_i x_i)\), where \(b\) is a bias term, \(w_i\)'s are some weights, and \(f\) is the Heaviside step function. In machine learning literature, \(f\) is known as activation function. More concisely, \(f({\bf x}) = 1_{x^Tw+b > 0}\). This construction can be used for solving dichotomous classification problems.

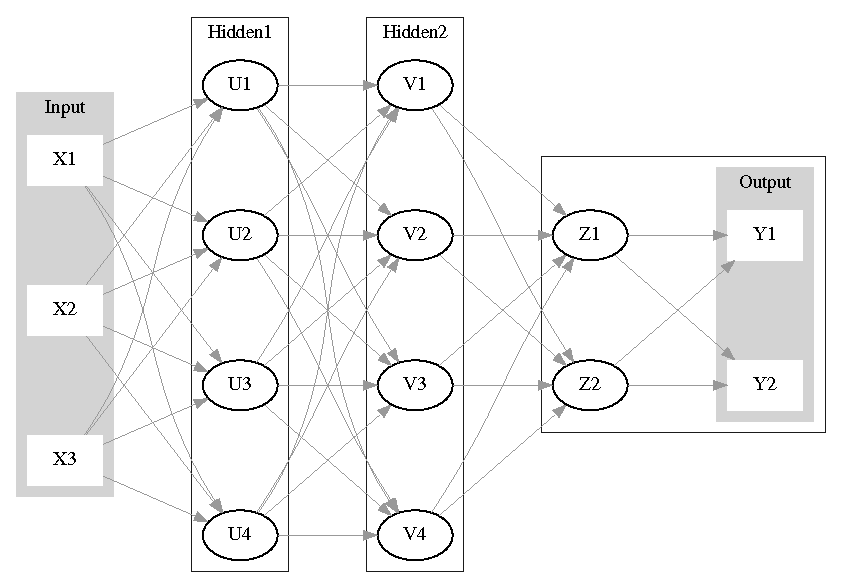
The inability of the original perceptron to resolve classes that are not linearly separable let to the development of perceptrons with 2 or more layers, different activation functions and multiclass output support. These multilayer models belong to the more general class of feed-forward artificial networks.

The mlp2 command implements 3-level multilayer perceptron. Excluding the input, the model has 2 hidden layers and an output layer. It is formally defined by the following set of equations. Let \(x_i\), \(i=1,\dots,p\) be the input variables, \(u_j\), \(j=1,\dots,m_1\) be the variables of the first hidden layer, \(v_k\), \(k=1,\dots,m_2\) be variables of the second layer, and \(y_l\), \(l=1,\dots,c\) be the output class variables, then

\begin{align} \begin{split} u_j = ReLU(\alpha_{0j} + \sum_{i=1}^p \alpha_{ij} x_i),\textrm{ }j=1,\dots,m_1 \\
v_k = ReLU(\beta_{0k} + \sum_{j=1}^{m_1} \beta_{jk} u_j),\textrm{ }k=1,\dots,m_2 \\
z_l = \gamma_{0l} + \sum_{k=1}^{m_2} \gamma_{kl} v_k,\textrm{ }l=1,\dots,c \\
y_l = f_l(z),\textrm{ }l=1,\dots,c \end{split} \end{align}

where \(ReLU\) is the rectified linear unit function, \(ReLU(x) = \max\{0, x\}\). Ddue to its effectiveness in practice, \(ReLU\) became a preferred activation function in feed-forward networks. The function \(f\) depends on the type of the outcome \(y\). mlp2 supports 2 choices: softmax and mse.

The softmax function is suitable for categorical outcome and has the form \begin{align} \begin{split} f_l(z) = \frac{\exp(z_l)}{\sum_{q=1}^c \exp(z_q)},\textrm{ } l=1,\dots,c \end{split} \end{align}

It is based on the multinomial logistic regression model. Given a training sample \(\{(x^s, y^s)\}_{s=1}^n\), the softmax loss value is given by the negative log-likelihood of parameters \({z_l^s}\) with respect to the sample

\begin{align} \begin{split} softmax: \sum_{s=1}^n \Bigl\{ \log\Bigl(\sum_{l=1}^c \exp(z_l^s)\Bigr) - z_{y^s}^s \Bigr\} / n \end{split} \end{align} The loss is an implicit function of all model parameters \(\alpha\), \(\beta\), and \(\gamma\). The total number of parameters in this case is \(m_1(p+1)+m_2(m_1+1)+c(m_2+1)\).

The mse loss is suitable for continuous outcome. In this case \(c=1\) and \(f\) is the identity function, i.e. \(y = z\). The mse loss has the form \begin{align} \begin{split} mse: \sum_{s=1}^n (z^s - y^s )^2 / n \end{split} \end{align}

The training involves finding a set of parameters that minimize the loss function. Note that the loss function is non-convex in general and may not have a global minimum. So we should look for a pragmatic solution - a set of optimal parameters such that the model generalizes well to new data in terms of prediction accuracy. The mainstream method for learning multilayer perceptrons, and feed-forward networks in general, is stochastic gradient descent and its derivatives. The gradients are computed using the backpropagation algorithm, [²].

In Figure 1 I show an example of perceptron that can be specified using the mlp2 command. It has 3 input variables, 2 hidden layers with 4 neurons each, and a 2-class output, that is, the output layer implements logistic regression.

Command description

The mlp2 fit command is used for model specification and training. You start by identifying the dependent and independent variables. As a minimum you also need to specify the size of the hidden layers using the layer1() and layer2() options. In rare cases when the default choice of loss function is not what you want, you may change it using the loss() option. The default choice for optimizer is sgd, a stochastic gradient descent optimizer, which you can change with the optimizer() option. Then you may need to think about other optimization-specific options such as learning rate lrate(), batch size batch(), maximum number of optimization iterations epochs(), etc. Usually you need several runs of mlp2 fit followed by some validation assessment in order to find optimal optimization regime.

The mlp2 predict command performs prediction and reports a performance score. You need to provide a stub for the prediction variables using the genvar() option. You also have the option to specify a ground-truth variable using truelabel(). If not supplied, the training outcome variable name is used, if such variable exists in the current dataset.

In case of categorical outcome, the mlp2 predict command creates as many prediction variables as are the number of outcome classes and these contain the prediction probabilities for each class. The prediction accuracy is calculated by comparing the most probable predicted class with the true class. In case of continuous outcome, one prediction variable is created that holds predicted values in the original scale of the outcome. The performance metrics is determined by the type of the outcome: accuracy acc, for categorical outcome, and mean absolute error mae, for continuous outcome.

When prediction is performed on the sample used for training we have in-sample prediction. In-sample prediction cannot be used for over-fitting estimation and it is thus not useful for validation. A common strategy is to divide the current dataset into 2 samples, one used for training and the other for validation. This can be done using if/in statements. You can also call mlp2 predict on a completely new dataset, if you believe that the model you have trained is compatible with the new data. For the purpose, you may need to supply a new set of independent variables, if they differ from the original independent variable names used for training. Of course, the provided independent and ground-truth variables must be compatible with their training counterparts in order for the prediction to make sense.

Example

I show an application of mlp2 using the Health Insurance dataset sysdsn1 available in Stata

. webuse sysdsn1

Lets say we want to model the insure binary outcome by the independent variables age, male, nonwhite, and site. Lets first look at these variables. The summary shows that the insure variable has 28 missing values and age has 1. The observations with missing values will be automatically dropped during training.

. summarize insure age male nonwhite site

    Variable |        Obs        Mean    Std. Dev.       Min        Max
-------------+---------------------------------------------------------
      insure |        616    1.595779    .6225427          1          3
         age |        643    44.41415    14.22441   18.11087   86.07254
        male |        644    .2593168    .4386004          0          1
    nonwhite |        644    .1956522    .3970103          0          1
        site |        644    1.987578    .7964742          1          3

Next, I call the mlp2 fit command to train a multilayer perceptron with hidden layers having 100 neurons each. All options, except the layer options, are left at their default values.

. mlp2 fit insure age male nonwhite i.site, layer1(100) layer2(100)
(28 missing values generated)

------------------------------------------------------------------------------
Multilayer perceptron                              input variables =        4
                                                   layer1 neurons  =      100
                                                   layer2 neurons  =      100
Loss: softmax                                      output levels   =        3

Optimizer: sgd                                     batch size      =       50
                                                   max epochs      =      100
                                                   loss tolerance  =    .0001
                                                   learning rate   =       .1

Training ended:                                    epochs          =       56
                                                   start loss      =  1.23665
                                                   end loss        =  .820173
------------------------------------------------------------------------------

The output is broken into 3 parts. First is displayed model specific information such as the number of input variables, the number of neurons in the hidden layers, the number of output levels, and the applied loss function. In the second block, we see the choice of optimizer with other optimization specific information such as batch size, maximum number of epochs, learning rate, etc. The third block is displayed after the optimization ends and shows the actual number of epochs and the starting and ending loss values.

We see that the mlp2 fit command performed 56 optimization steps and the initial loss of 1.24 has been reduced to 0.82. However, the optimization loss has itself is not very informative for the goodness of fit of the model.

I can use the mlp2 predict command to perform in-sample prediction. I specify the genvar(pr) option to supply a stub for the variables that will hold the class predicted probabilities: pr_Indemnity, pr_Prepaid, and pr_Uninsure. I also indicate the true outcome variable, insure, in order to compare and calculate the prediction performance, although this is not needed because insure is the outcome variables used during training.

. mlp2 predict, genvar(pr) truelabel(insure)
(28 missing values generated)

Prediction accuracy: .5902439024390244

The achieved in-sample accuracy is only 59% which does not seem terribly good, but it is still much better than the 33% accuracy of a random choice prediction. Keep in mind that mlp2 is not expected to work well out of the box and tweaking the model and optimization options is often necessary.

Lets inspect some of the predicted probabilities and the actual outcome

. list pr* insure in 1/10

     +--------------------------------------------+
     | pr_Ind~y   pr_Pre~d   pr_Uni~e      insure |
     |--------------------------------------------|
  1. | .6729499    .299127   .0279232   Indemnity |
  2. | .3853745   .5955154   .0191101     Prepaid |
  3. | .5070527   .4075416   .0854058   Indemnity |
  4. | .2121731   .7453947   .0424322     Prepaid |
  5. |        .          .          .           . |
     |--------------------------------------------|
  6. | .4088286   .5706751   .0204963     Prepaid |
  7. | .5355542   .4351238   .0293221     Prepaid |
  8. |        .          .          .           . |
  9. | .4998144   .3933753   .1068103    Uninsure |
 10. | .4626809   .4840307   .0532884     Prepaid |
     +--------------------------------------------+

As we see, except cases 5, 8, and 9, the true outcome is predicted with highest probability. Of course, in-sample prediction is not a good way to evaluate the model fit and we should use independent sample to do so. I shall illustrate this elsewhere.

More applications of mlp2

See the this post for an application of mlp2 to image data.

References